Какие числа называются целыми

Целые числа — это фундаментальная концепция в математике, которая формирует основу для понимания множества других математических понятий. Они включают в себя как положительные числа, так и отрицательные, а также ноль. Целые числа используются в самых различных областях: от базовых арифметических операций до сложных математических теорий и приложений в реальной жизни.

Определение целых чисел

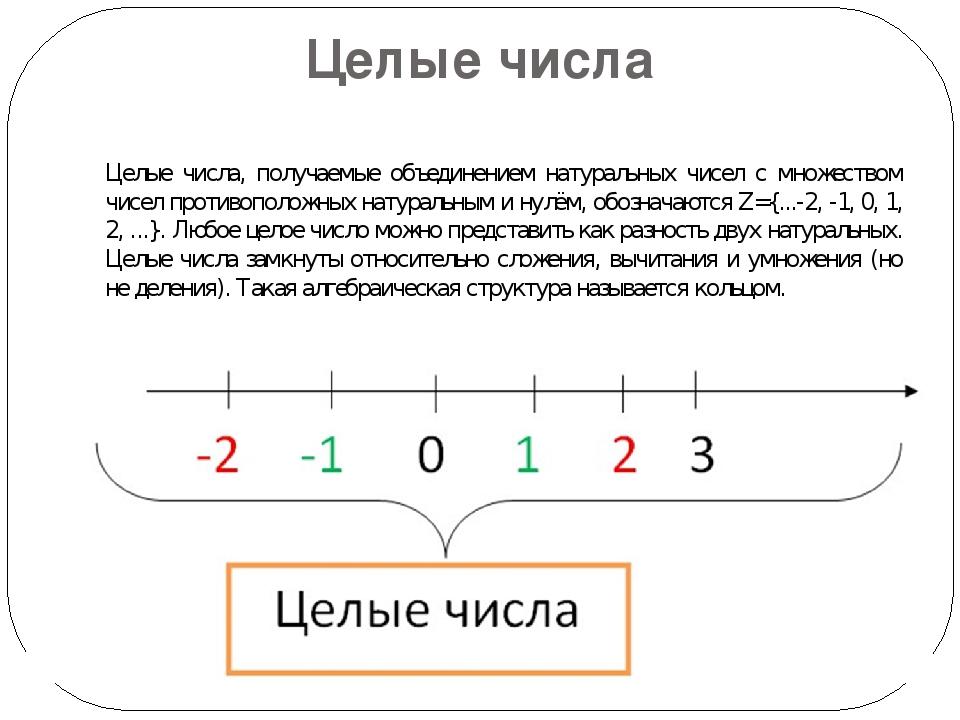
Целые числа можно определить как все числа, которые не имеют дробной или десятичной части. Это включает в себя как положительные числа, которые идут от единицы и выше (например, 1, 2, 3, 4 и так далее), так и отрицательные числа (например, -1, -2, -3, -4 и так далее). Ноль, который не является ни положительным, ни отрицательным числом, также относится к целым числам. Таким образом, множество целых чисел можно представить в виде бесконечной последовательности: …, -3, -2, -1, 0, 1, 2, 3, …

Историческая справка и развитие концепции

Исторически, концепция целых чисел развивалась постепенно. В древности математики использовали только положительные числа для счетных операций. Однако с развитием математических исследований и потребностью в решении более сложных задач стало очевидным, что необходимо расширить эти числа для включения отрицательных значений. Например, в Индии и Китае уже в средние века начали использовать отрицательные числа для решения уравнений. В Европе же такая идея была воспринята лишь в Новое время, когда математики, такие как Кардано и Вьет, начали активно использовать отрицательные корни в своих работах.

Целые числа в современном контексте

В современной математике целые числа играют ключевую роль. Они являются основой для изучения более сложных числовых систем, таких как рациональные числа (которые включают дроби) и иррациональные числа. Целые числа также широко применяются в различных областях науки и техники. В компьютерных науках они используются для представления данных, индексации массивов и выполнения арифметических операций. В экономике и статистике целые числа применяются для подсчета и анализа данных.

Роль целых чисел в математике

Целые числа являются основой для многих математических операций и теорий. Они играют важную роль в арифметике, алгебре и теории чисел. Например, операции сложения, вычитания и умножения целых чисел ведутся по строго определенным правилам, которые служат основой для более сложных математических понятий. Кроме того, целые числа помогают определить свойства делимости и кратности, которые являются важными аспектами в теории чисел.

Таким образом, целые числа являются важнейшим элементом математической науки, обладая фундаментальными свойствами и широким спектром применения. Понимание их определений, свойств и исторического развития помогает глубже осознать их роль в различных математических и практических задачах.

Классификация целых чисел

Целые числа можно классифицировать на несколько основных категорий, каждая из которых играет свою роль в математике и реальной жизни. Для лучшего понимания и изучения можно воспользоваться курсами по математике, после которых вы уже будете знать что такое целые числа. Понимание этих категорий помогает лучше ориентироваться в числовых системах и проводить математические операции.  Данной классификации выделяются следующие группы целых чисел:

Положительные целые числа

• Определение: Положительные целые числа — это числа, которые больше нуля и не имеют дробной части. Они представляют собой основную часть множества целых чисел и включают числа 1, 2, 3, 4 и так далее, бесконечно в возрастающем порядке.
• Примеры: 1, 5, 23, 100.
• Применение: Положительные целые числа используются в различных областях, таких как подсчет объектов, измерение количеств и определение позиций. Они играют ключевую роль в арифметике и базовых математических операциях.

Отрицательные целые числа

• Определение: Отрицательные целые числа — это числа, которые меньше нуля и также не имеют дробной части. Они представляют собой отрицательную часть множества целых чисел и включают числа -1, -2, -3, -4 и так далее, бесконечно в убывающем порядке.
• Примеры: -1, -7, -20, -100.
• Применение: Отрицательные целые числа используются для обозначения убытков, дефицита, температур ниже нуля и других ситуаций, где необходима величина, меньше нуля.

Ноль

• Определение: Ноль — это особое целое число, которое не является ни положительным, ни отрицательным. Оно играет уникальную роль в системе целых чисел, служа границей между положительными и отрицательными числами.
• Примеры: 0.
• Применение: Ноль используется как исходная точка отсчета, в уравнениях, где он может служить нейтральным элементом при сложении и вычитании, а также в различных математических операциях, таких как умножение и деление.

Соотношения между группами

• Положительные и отрицательные целые числа: Эти группы являются противоположностями, и каждая отрицательная величина имеет соответствующее положительное значение и наоборот. Например, -5 и 5 являются взаимно противоположными числами.
• Ноль как граница: Ноль находится на границе между положительными и отрицательными целыми числами, и его можно рассматривать как «нейтральную» точку, которая не входит ни в одну из двух категорий.

Примеры целых чисел в различных областях

Целые числа играют ключевую роль в множестве областей, от повседневных задач до сложных научных исследований. Вот несколько примеров их применения в различных сферах:

1. Повседневная жизнь

• Финансовые транзакции: При ведении личного бюджета целые числа используются для учета доходов и расходов. Например, если у вас есть 1500 рублей, а вы потратили 450 рублей, то остаток составляет 1050 рублей.
• Подсчет объектов: Целые числа применяются для подсчета предметов в магазине, таких как яблоки или книги. Например, в магазине может быть 25 яблок, и если продано 7, то на складе останется 18 яблок.
• Оценки и рейтинги: В школах и университетах оценки часто выражаются целыми числами. Например, оценка «4» может означать хороший уровень знаний по предмету.

2. Математика

• Арифметика и алгебра: В базовой арифметике целые числа используются для операций сложения, вычитания, умножения и деления. Например, уравнение $7-3=4$ демонстрирует использование целых чисел.
• Теория чисел: Целые числа играют важную роль в теории чисел, изучении их свойств и закономерностей. Примеры включают простые числа, такие как 2, 3, 5 и 7.

3. Наука и инженерия

• Физика: Целые числа могут использоваться для обозначения уровней энергии или состояния системы. Например, в квантовой механике состояние электрона в атоме может обозначаться целым числом, указывающим на уровень энергии.
• Инженерия: При проектировании зданий или машин целые числа применяются для расчета размеров, количества материалов и других параметров. Например, если требуется 50 болтов для конструкции, это число является целым.

4. Компьютерные науки

• Программирование: В программировании целые числа используются для представления данных, управления потоками программы и выполнения арифметических операций. Например, в программировании индекс массива часто представляется целым числом.
• Базы данных: Целые числа применяются для идентификации записей в базе данных, таких как уникальные идентификаторы (ID) пользователей или заказов.

5. Экономика и статистика

• Анализ данных: Целые числа используются для представления количественных данных, таких как количество проданных товаров или численность населения. Например, если город имеет население 1,200,000 человек, это число является целым.
• Экономическое планирование: При составлении бюджета и планировании затрат целые числа могут обозначать суммы денег, количество товаров и другие параметры. Например, если планируется покупка 150 единиц товара, это число целое.

Свойства целых чисел

Целые числа обладают рядом важных свойств, которые играют ключевую роль в математике и её приложениях. Эти свойства касаются операций с целыми числами, их сравнений и других математических характеристик. Вот основные свойства целых чисел:

1. Замкнутость

• Свойство: Целые числа замкнуты относительно операций сложения, вычитания и умножения. Это означает, что результат выполнения этих операций над любыми двумя целыми числами снова будет целым числом.
• Примеры:
  • Сложение: $3+4=7$, где 3 и 4 — целые числа, и их сумма 7 также является целым числом.
  • Вычитание: $7-5=2$, где 7 и 5 — целые числа, и разность 2 также является целым числом.
  • Умножение: $4\times 6=24$, где 4 и 6 — целые числа, и их произведение 24 также является целым числом.

2. Свойство дистрибутивности

• Свойство: Умножение целых чисел распределяется относительно сложения и вычитания. Это означает, что умножение числа на сумму или разность двух других чисел можно распределить на каждое из чисел по отдельности.
• Формула: $a\times (b+c)=(a\times b)+(a\times c)$ и $a\times (b-c)=(a\times b)-(a\times c)$
• Пример:
  • $3\times (4+5)=(3\times 4)+(3\times 5)=12+15=27$

3. Свойство ассоциативности

• Свойство: Операции сложения и умножения целых чисел ассоциативны, что означает, что способ группировки чисел не влияет на результат.
• Формула:
  • Сложение: $(a+b)+c=a+(b+c)$
  • Умножение: $(a\times b)\times c=a\times (b\times c)$
• Примеры:
  • $(2+3)+4=2+(3+4)=9$
  • $(2\times 3)\times 4=2\times (3\times 4)=24$

4. Свойство коммутативности

• Свойство: Операции сложения и умножения целых чисел коммутативны, что означает, что порядок чисел не влияет на результат.
• Формула:
  • Сложение: $a+b=b+a$
  • Умножение: $a\times b=b\times a$
• Примеры:
  • $5+7=7+5=12$
  • $4\times 6=6\times 4=24$

5. Нейтральные элементы

• Свойство:
  • Сложение: Нейтральным элементом при сложении является ноль. Для любого целого числа $a$, $a+0=a$.
  • Умножение: Нейтральным элементом при умножении является единица. Для любого целого числа $a$, $a\times 1=a$.
• Примеры:
  • $8+0=8$
  • $7\times 1=7$

6. Свойство обратимости

• Свойство:
  • Сложение: Каждое целое число $a$ имеет противоположное целое число, называемое его обратным элементом при сложении, так что $a+(-a)=0$.
  • Умножение: Каждое целое число $a$, отличное от нуля, имеет обратный элемент при умножении, который равен $1/a$. Однако для целых чисел этот элемент тоже является целым числом только в случае, если $a$ равно ±1.
• Примеры:
  • Обратный элемент при сложении: $5+(-5)=0$
  • Обратный элемент при умножении: Для 2 и -2 (кроме нуля): 2×12=12 \times \frac{1}{2} = 12×21​=1, но это не целое число.

7. Свойство порядка

• Свойство: Целые числа можно упорядочить по величине. Если $a$ и $b$ — целые числа, то $a<b$, $a=b$ или $a>b$.
• Примеры:
  • Если $-3<0$ и $0<7$, то $-3<7$.

Выводы о целых числах

Целые числа — это основополагающий элемент математики, имеющий множество важных свойств и применений в различных областях. Рассмотрев их ключевые характеристики и свойства, можно сделать следующие выводы:

1. Фундаментальная природа целых чисел Целые числа формируют основную числовую систему, которая включает в себя положительные числа, отрицательные числа и ноль. Эти числа являются базой для более сложных математических понятий и операций. Их простота и универсальность делают их неотъемлемой частью как базовой арифметики, так и более сложных математических дисциплин.
2. Свойства целых чисел обеспечивают их гибкость и полезность Свойства целых чисел, такие как замкнутость, дистрибутивность, ассоциативность и коммутативность, делают их крайне удобными для выполнения математических операций. Эти свойства позволяют легко и эффективно работать с числами при решении уравнений, анализе данных и моделировании различных процессов.
3. Целые числа применяются в широком спектре областей Примеры использования целых чисел охватывают повседневную жизнь, математику, науку, инженерные задачи, программирование и экономику. От подсчета товаров в магазине до анализа данных и разработки программного обеспечения — целые числа играют ключевую роль в этих процессах.
4. Целые числа помогают формировать логическое мышление Изучение свойств и применения целых чисел развивает аналитическое и логическое мышление. Понимание их свойств и особенностей помогает формировать навыки решения задач, критического мышления и применения математических знаний на практике.
5. Развитие концепции целых чисел связано с историческим контекстом Историческое развитие концепции целых чисел демонстрирует эволюцию математических идей и их адаптацию к потребностям различных культур и эпох. Изучение этого развития помогает лучше понять, как современные математические понятия формировались и как они применяются сегодня.

Заключение

Целые числа являются основой математической науки и имеют широкое применение в различных областях. Их свойства и характеристики делают их мощным инструментом для решения множества практических и теоретических задач. Понимание и использование целых чисел — важный аспект не только для обучения математике, но и для успешной деятельности в многих профессиональных областях.